Cos 2x O O tan 2xFormulas and identities of sin 2x, cos 2x, tan 2x, cot 2x, sec 2x and cosec 2x are known as double angle formulas because they have angle double of the angle present in their formulas Sin 2x Formula Sin 2x formula is 2sinxcosx Image will be uploaded soon Sin 2x =2 sinx cosx Derivation of Sin2x Formula Before going into the actual proofIf we continue, with n=3, H=2·tan x, K=1−tan 2 x, using the formula we have tan 3x=(2·tan xtan x (as apposed to the previous two terms for the sine and cosine formulae) Proof That we have chosen to claim to prove the formula for all integers, n, neither implies nor does not imply the truth of the equations for rational, real or

Tan2x Sin2x Tan2x Sin2x 5 1 Brainly In
Tan 2x formula in terms of sin x
Tan 2x formula in terms of sin x-Solve for x tan (2x)=1 tan (2x) = 1 tan ( 2 x) = 1 Take the inverse tangent of both sides of the equation to extract x x from inside the tangent 2x = arctan(1) 2 x = arctan ( 1) The exact value of arctan(1) arctan ( 1) is π 4 π 4 2x = π 4 2 x = π 4 Divide each term by 2Cos 2x ≠ 2 cos x;




5 5 Multiple Angle And Product Sum Formulas Find All Solutions In Ppt Download
The sum and difference formulas allow expanding the sine, the cosine, and the tangent of a sum or a difference of two angles in terms of sines and cosines and tangents of the angles themselves These can be derived geometrically, using arguments that date to Ptolemy One can also produce them algebraically using Euler's formula SumFormula sin 2 θ = 2 tan θ 1 tan 2 θ A trigonometric identity that expresses the expansion of sine of double angle function in terms of tan function is called the sine of double angle identity in tangent function\(\cos 2X = \cos ^{2}X – \sin ^{2}X \) Hence, the first cos 2X formula follows, as \(\cos 2X = \cos ^{2}X – \sin ^{2}X\) And for this reason, we know this formula as double the angle formula, because we are doubling the angle Other Formulae of cos 2X \(\cos 2X = 1 – 2 \sin ^{2}X \) To derive this, we need to start from the earlier derivation
Tan 2x Formula Tan 2x is an important trigonometric function Tan 2x formula is one of the very commonly used double angle trigonometric formulas and can be expressed in terms of different trigonometric functions such as tan x, cos x, and sin xMath Calculus Calculus questions and answers 12 Find sin 2x, cos2x, and tan 2x if tanx= and x terminates in quadrant IV 5 0/0 님 sin 2x II 0 х Х $ ?Cos 2x = cos2 x – sin2 x = 1 – 2 sin2 x = 2 cos2 x – 1 • Tangent tan 2x = 2 tan x/1 tan2 x = 2 cot x/ cot2 x 1 = 2/cot x – tan x tangent doubleangle identity can be accomplished by applying the same methods, instead use the sum identity for tangent, first • Note sin 2x ≠ 2 sin x;
Is best understood in terms of another geometrical construction, the unit circle One can de ne De nition (Cosine and sine) Given a point on the unit circle, at a counterclockwise angle from the positive xaxis, cos is the xcoordinate of the point sin is the ycoordinate of the point tan 2x = ((2sin x)/(1 2sin^2 x))sqrt(1 sin ^2 x) sin 2x = (sin 2x)/(cos 2x) Applying the 3 trig identities sin 2x = 2sin xcos x , and cos 2x = (1 2sin^2 x) cos x = sqrt(1 sin^2 x) We get tan 2x = (2sin xcos x)/(1 2sin^2 x) = = ((2sin x)/(1 2sin^2 x))sqrt(1 sin^2 x) Transcript These formulas can be derived using x y formulas For sin 2x sin 2x = sin (x x) Using sin (x y) = sin x cos y cos x sin y = sin x cos x sin x cos



If Sin 3x Cos X Then Find Tan 2x Quora




Integrate Sec 2x Method 2
Simplify\\frac {\sec (x)\sin^2 (x)} {1\sec (x)} simplify\\sin^2 (x)\cos^2 (x)\sin^2 (x) simplify\\tan^4 (x)2\tan^2 (x)1 simplify\\tan^2 (x)\cos^2 (x)\cot^2 (x)\sin^2 (x) trigonometricsimplificationcalculator enHalfAngle Formulas sin 2 = q 1 cos 2 cos 2 = q 1cos 2 tan 2 = q 1cos tan 2 = 1 cosx sinx tan 2 = sin 1cos DoubleAngle Formulas sin2 = 2sin cos cos2 = cos2 sin2 tan2 = 2tan 1 tan2 cos2 = 2cos2 1 cos2 = 1 2sin2 ProducttoSum Formulas sinxsiny= 1 2 cos(x y) cos(x y) cosxcosy= 2 cos(x y) cos(x y) sinxcosy= 1 2 sin(x y) sin(x yWe know that the addition formula for sin is given as \(Sin (X Y) = Sin X Cos Y Cos X Sin Y,\) Where X and Y are the two angles In the above formula replace Y by X, with the assumption that both angles X and Y are equal Thus, \(Sin (XX) = Sin X Cos X Cos X Sin Y\) Hence Sin 2x = 2 Sin x Cos x Solved Examples for Sin 2x Formula




bestpictjcry Tan 2x Tan 2x



What Is The Formula Of Tan2x Quora
In Trigonometry Formulas, we will learn Basic Formulas sin, cos tan at 0, 30, 45, 60 degrees Pythagorean Identities Sign of sin, cos, tan in different quandrants Radians Negative angles (EvenOdd Identities) Value of sin, cos, tan repeats after 2π Shifting angle by π/2, π, 3π/2 (CoFunction Identities or Periodicity Identities)The double angle formulas can be derived by setting A = B in the sum formulas above For example, sin(2A) = sin(A)cos(A) cos(A)sin(A) = 2sin(A)cos(A) It is common to see two other forms expressing cos(2A) in terms of the sine and cosine of the single angle A Recall the square identity sin 2 (x) cos 2 (x) = 1 from Sections 14 and 23X Therefore, tan 2 x = ( sin 2 x / 1 − 2 sin 2 x) Is it possible to do it in terms of cos




Tan2x Formula In Terms Of Tan Edurev Class 12 Question




Challenge Trigonometric Equation Tan2x 8 Cos 2x Cot X Youtube
Tan2x Formula Sin 2x, Cos 2x, Tan 2x is the trigonometric formulas which are called as double angle formulas because they have double angles in their trigonometric functions Let's understand it by practicing it through solved example T an2x = 2tanx 1−tan2x T a n 2 x = 2 t a n x 1 − t a n 2 x243 The Substitution z = tan (x / 2) Suppose our integrand is a rational function of sin (x) and cos (x) After the substitution z = tan (x / 2) we obtain an integrand that is a rational function of z, which can then be evaluated by partial fractions Theorem If z = tan (x / 2), thenTan 2x ≠ 2 tan x




Sample Problems Cos 2 X Tan2 X Tan 2 Csc 2 Tan Sec X Tan X Cos X Sin 4 X Cos 4 X 1 2 Cos 2 X Pdf Free Download




Tan2x Sin2x Tan2x Sin2x 5 1 Brainly In
The tangent formula is easy to get just divide But it turns out to be easier if you don't divide the final forms, but rather the "raw" collected terms from above sin 3A = 3 cos² A sin A − sin³ A cos 3A = cos³ A − 3 cos A sin² A tan 3A = sin 3A / cos 3A tan 3A = (3 cos² A sin A − sin³ A) / (cos³ A − 3 cos A sin² A)Tan(2x) is a doubleangle trigonometric identity which takes the form of the ratio of sin(2x) to cos(2x) sin(2 x ) = 2 sin( x ) cos( x ) cos(2 x ) = (cos( x ))^2 – (sin( x ))^2 = 1 – 2 (sin( x ))^2 = 2 (cos( xTo rewrite the sine function in terms of tangent, follow these steps Start with the ratio identity involving sine, cosine, and tangent, and multiply each side by cosine to get the sine alone on the left Replace cosine with its reciprocal function Solve the Pythagorean identity tan 2




Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x




Multiple Angle Formulas Es Demonstrating Understanding Of Concepts Warm Up Use A Sum Formula To Rewrite Sin 2x In Terms Of Just Sin X Cos X Do Ppt Download
Rewrite sec(x) sec ( x) in terms of sines and cosines Rewrite tan(x) tan ( x) in terms of sines and cosines Multiply by the reciprocal of the fraction to divide by 1 cos(x) 1 cos ( x) Write cos(x) cos ( x) as a fraction with denominator 1 1 Cancel the common factor of cos(x) cos ( x) 2 tanx 1 − tan2x = 2 sinx cosx 1 − ( sin2x cos2x) = 2sinx cosx cos2x −sin2x = sin2x cos2x = tan2x Proofs for sin2x = 2sinxcosx and cos2x = 1 −2sin2x Use Area of a ABC = 1/2 (base) (altitude) = 1/2 bc sin A Here, it is the ABC of a unit circle, withThe identity 1 cot 2 θ = csc 2 θ 1 cot 2 θ = csc 2 θ is found by rewriting the left side of the equation in terms of sine and cosine for all θ θ in the domain of the tangent function 1 sin 2 x cos 2 x = 1 cos 2 x sin 2 x cos 2 x = 1 2 tan 2 x 1 sin 2 x cos 2 x = 1 cos 2 x sin 2 x cos 2 x = 1 2 tan 2 x 32 (sin x




Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube
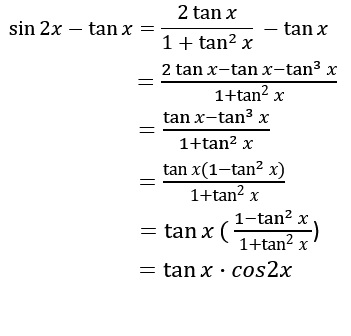



Sin2x Tanx Complete The Identity Socratic
TRIGONOMETRY LAWS AND IDENTITIES DEFINITIONS sin(x)= Opposite Hypotenuse cos(x)= Adjacent Hypotenuse tan(x)= Opposite Adjacent csc(x)= Hypotenuse Opposite sec(x)= Hypotenuse Adjacent Since t = tan(x / 2) = sin ( x / 2) cos ( x / 2) and sin2(x / 2) cos2(x / 2) = 1, solve for sin(x / 2) = t √1 t2 and cos(x / 2) = 1 √1 t2 (here I am assuming that x / 2 ∈ 0, π / 2) the other cases are similar) Now you can use the formulas that give you the sin and cos of double angles, and you are done Share Sin2x=Tan2x/Sqrt(1tan^2(2x)) this is all ok but sin2x=2sinxcosx so you need to do the same for cos2x and find cosx in terms of tan2x thus replace it into the expression above I hope this helps
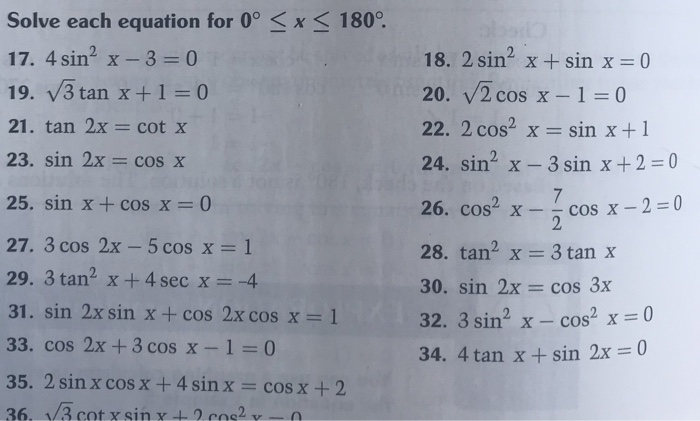



Solved Solve Each Equation For 0 X 180 17 4 Sin2 X 3 0 Chegg Com




Tangent Half Angle Formula Wikipedia
We will develop formulas for the sine, cosine and tangent of a half angle Half Angle Formula Sine We start with the formula for the cosine of a double angle that we met in the last section cos 2θ = 1− 2sin 2 θQ3Find a polynomial approximation of the function sec2(x) Q4Find a polynomial approximation of the function sin2(x)cos(x)tan(x) Q5For the function f(x)=sec(x)(sin(x)cos(x)) (a) Find a polynomial approximation of f(x) using the standard small angle approximations (b) Find a polynomial approximation of f(x) using sin(x) ˇx and theThe range of cscx is the same as that of secx, for the same reasons (except that now we are dealing with the multiplicative inverse of sine of x, not cosine of x)Therefore the range of cscx is cscx ‚ 1 or cscx • ¡1 The period of cscx is the same as that of sinx, which is 2Since sinx is an odd function, cscx is also an odd function Finally, at all of the points where cscx is




Maths Lover Maths Lover Added A New Photo




Write Cos2x In Tan And Prove Trigonometric Identity For Double Angle Youtube
Sine, tangent, cotangent, and cosecant are odd functions while cosine and secant are even functions sin –t = –sin t cos –t = cos t tan –t = –tan t Sum formulas for sine and cosine sin (s t) = sin s cos t cos s sin t cos (s t) = cos s cos t – sin s sin t Double angle formulas for sine and cosine sin 2t = 2 sin t cos tIn this video, I derive the following identitiessin(x) = 2*t / (1 t^2)cos(x) = (1 t^2) / (1 t^2)These identities are important when it comes to simpliFormulas from Trigonometry sin 2Acos A= 1 sin(A B) = sinAcosB cosAsinB cos(A B) = cosAcosB tansinAsinB tan(A B) = A tanB 1 tanAtanB sin2A= 2sinAcosA cos2A= cos2 A sin2 A tan2A= 2tanA 1 2tan A sin A 2 = q 1 cosA 2 cos A 2



3




Ex 2 2 13 Inverse Trigonometry Tan 1 2 Sin 1 2x 1 X2
sin (x)=cos (x)tan (x) At this point I realize this is assuming therefore, But I graphed this and it only looks right half of the time What I should have is the plus or minus when taking the root of cos 2 (x) but I need the plus half the time, and the minus the other half of the time and then merge them to describe sin (x) in terms of tan (x)The Pythagorean formula for tangents and secants There's also one for cotangents and cosecants, but as cotangents and cosecants are rarely needed, it's unnecessary Identities expressing trig functions in terms of their supplements Sum, difference, and double angle formulas for tangent The half angle formulas The ones for sine andThe cosine of double angle is equal to the quotient of the subtraction of square of tangent from one by the sum of one and square of tan function cos 2 θ = 1 − tan 2 θ 1 tan 2 θ It is called the cosine of double angle identity in terms of tangent function




Weierstrass Substitution Wikipedia



bestpictjcry Tan 2x Tan 2x
There are two basic formulas for sin 2x sin (2x) = 2 sin x cos x (in terms of sin and cos) sin (2x) = (2tan x)/ (1 tan2x) (in terms of tan) Double Angle Formulas The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself Tips for remembering the following formulas We can substitute the values ( 2 x) (2x) (2x) into the sum formulas for sin \sin sin andIdentities related to sin 2x, cos2x, tan 2x, sin3x, cos3x, and tan3x Sin 2x = Sin 2x = sin(2x)=2sin(x) cos(x) Sin(2x) = 2 * sin(x)cos(x) Proof To express Sine, the formula of "Angle Addition" can be used




Tan 2x Formula What Is Tan 2x Formula Examples



What Is Limit X 0 Tan2x X 3x Sinx Quora




5 5 Multiple Angle And Product Sum Formulas Find All Solutions In Ppt Download




Weierstrass Substitution Wikipedia



Example 28 If Tan X 3 4 Find Sin X 2 Cos X 2 Tan X 2



Trigonometric Functions Of Double Angles Expressed By The Tangent Function Trigonometric Functions Expressed By The Tangent Of The Half Angle Trigonometric Identities Examples




Inverse Trigonometric Functions General Solution Of
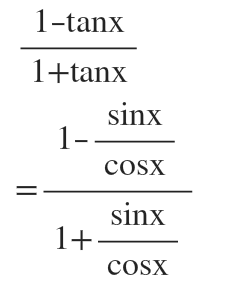



Answered Prove The Following Identity 1 Tan X Bartleby




Sin 2x Formula What Is Sin 2x Formula Examples



What Is The Proof Of Tan 3x Quora




Trig Identity Sec2x Minus Tan2x T10 Youtube




Tangent Half Angle Formula Wikipedia




Tan2x ただの悪魔の画像




Double Angle Formulas What Are Double Angle Formulas Examples




Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com




Packet 21 Trigonometric Identities Ppt Download




How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube



Tan2x 1 ただの悪魔の画像




Solve The Trigonometric Equation Tan X Tan 2x Tan X Tan 2x 1



What Is The Formula Of Tan2x Quora




Solved Verify The Identity 2 Tan X Sin 2x 1 Tan2 X 2 Chegg Com




Cos 2x Formula Derivation Examples What Is Cos 2a Formula




Tan2x Sec2x ただの悪魔の画像
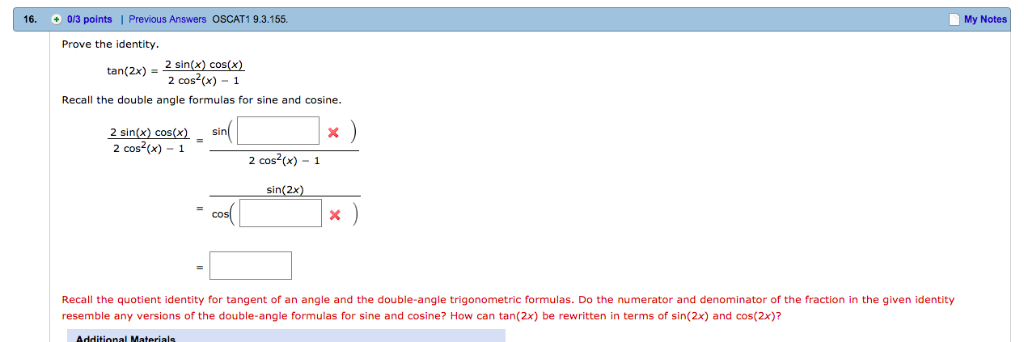



Solved 16 0 3 Points Previous Answers Oscat1 9 3 155 My Chegg Com




Tan2x ただの悪魔の画像




Answered 15 Find Sin 2x Cos 2x And Tan 2x If Bartleby




C9 Eeds7j7ncrm
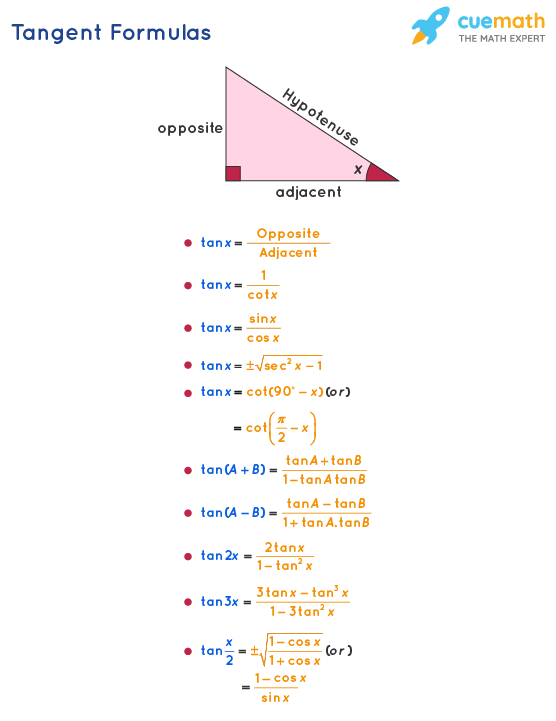



Tangent Formula What Are Tangent Formulas Examples




Ex 3 3 19 Prove Sin X Sin 3x Cos X Cos 3x Tan 2x




Expressing Sin X And Cos X In Terms Of T Tan X 2 Youtube




Tan2x ただの悪魔の画像




How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube




Solve The Following Equation Tan X Tan 2x Tan 3x 0
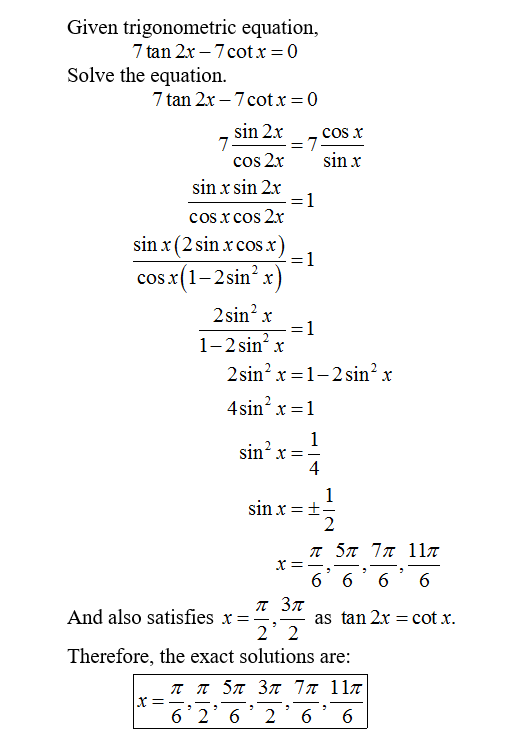



Solved Given Trigonometric Equation 7 Tan 2x 7 Cotx 0 Chegg Com
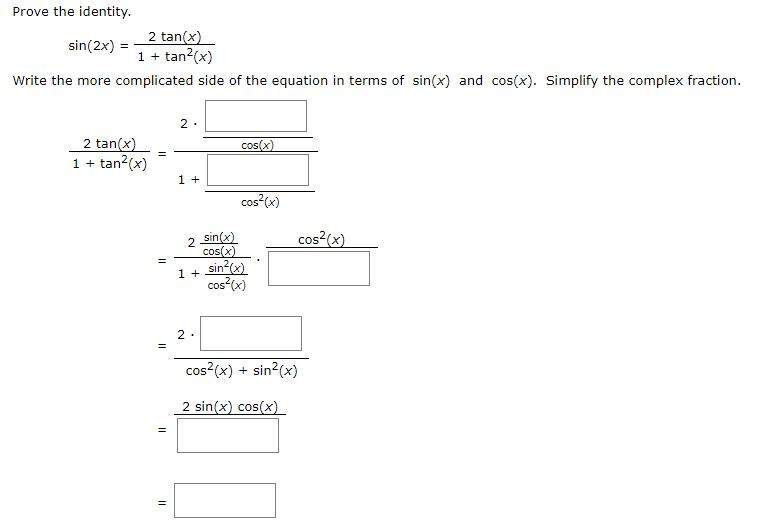



Solved Prove The Identity 2 Tan X Sin 2x 1 Tan2x Write Chegg Com




Misc 10 Sin X 1 4 Find Sin X 2 Cos X 2 Tan X 2 Chapter 3




Tan 2 X Tan 2 X 1 Cosec 2 X Sec 2 X Cosec 2 X 1 Sin 2 X Cos 2 X Brainly In
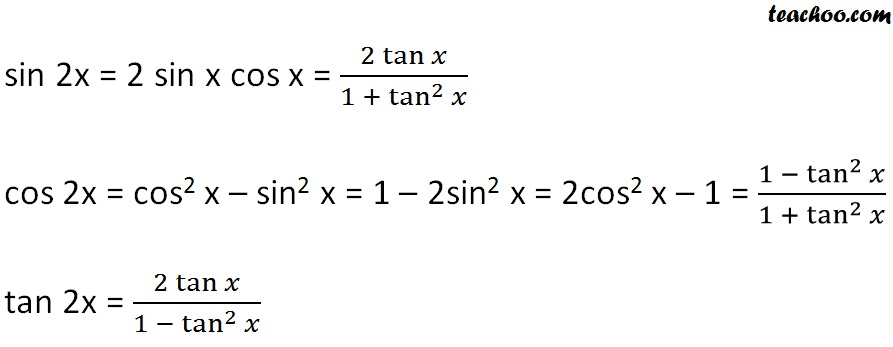



Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi




bestpictjcry Tan 2x Tan 2x




bestpictjcry Tan 2x Tan 2x



Trigonometric Functions Expressed By The Tangent Of The Half Angle Trigonometric Identities



What Is The Formula Of Tan2x Quora




Inttanx Tan2x Tan3x Dx Is Equal To



Sin3x




Tan2x Sec2x ただの悪魔の画像




Solved Prove The Identity 2 Sin X Cos X Tan 2x 2 Chegg Com




Multiple Angle Formulas Es Demonstrating Understanding Of Concepts Warm Up Use A Sum Formula To Rewrite Sin 2x In Terms Of Just Sin X Cos X Do Ppt Powerpoint



1
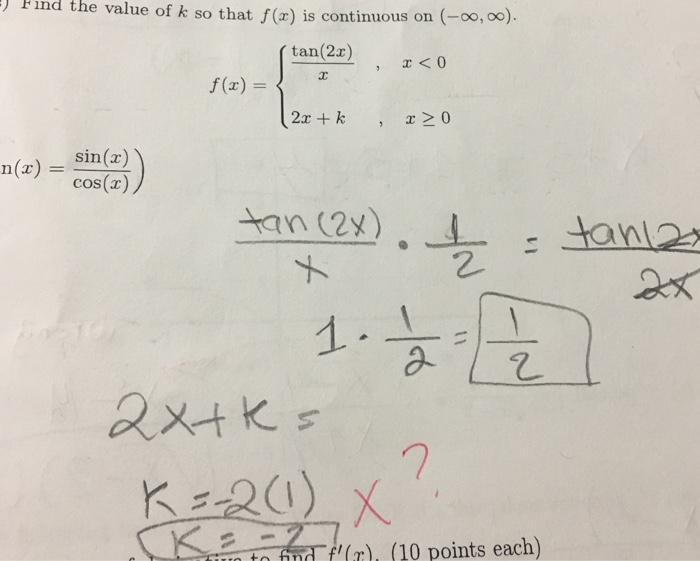



Solved Find The Value Of K So That F N Is Continuous On Chegg Com



Solved Consider The Possible Identity Tan 2x Cos 2x 1 Cos 2x Sec 2x A State Any Non Permissible Values B Attempt To Verify Possible Identity Course Hero




Calculate Sin2x Cos2x And Tan2x For Given Tanx In Quadrant 2 Youtube



3




Trig Graphs Investigate The Effects Of 2sin X 2cos X 2tan X Ppt Video Online Download




Tan 2x Sin 2x Tan 2x Sin 2x




bestpictjcry Tan 2x Tan 2x




If Sin X 5 3 And 0 Lt X Lt P 2 Find The Value Of Sin 2x Cos 2x Tan 2x Brainly In




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube




Fastest Sin2x Identity In Terms Of Tan




How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic




Misc 10 Sin X 1 4 Find Sin X 2 Cos X 2 Tan X 2




Solved Section 7 3 Double Angle Half Angle And Chegg Com



How To Find Sin2x Cos2x And Deduce Tan2x In Terms Of Tanx Only Quora




Example 28 If Tan X 3 4 Find Sin X 2 Cos X 2 Tan X 2



If Sin 3x Cos X Then Find Tan 2x Quora



What Is Integral Of Sin2x Tan2x Quora



Sin 2x Cos 2x And Tan 2x




Ppt Multiple Angle Formulas Ts Making Decisions After Reflection And Review Powerpoint Presentation Id




Analytic Trig Ppt Video Online Download
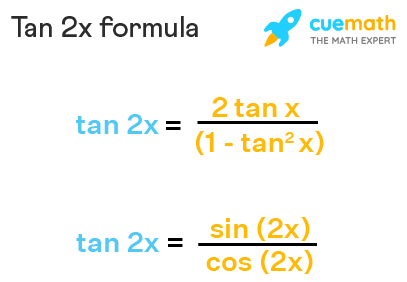



Tan 2x Formula What Is Tan 2x Formula Examples




How Do You Find A Double Angle Formula For Sec 2x In Terms Of Only Csc X And Sec X Socratic




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com




Tan2x 1 ただの悪魔の画像




Tangent Half Angle Formula Wikipedia



What Is The Value Of Sin 2x In Terms Of Tan X Quora




Example 28 If Tan X 3 4 Find Sin X 2 Cos X 2 Tan X 2




Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com




Double Angles Ppt Video Online Download




Expressing Sin X And Cos X In Terms Of T Tan X 2 Youtube
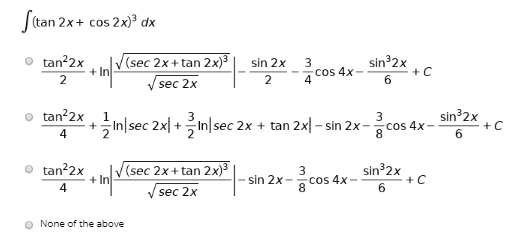



Answered Stan 2x Cos 2x Dx Tan 2x 2 V Sec 2x Bartleby




Tan2x ただの悪魔の画像




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic




Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube



0 件のコメント:
コメントを投稿